Optimizing Automatic Oil Spill Detection using a Genetic Algorithm

🗓 June 2016—March 2017

Project Link: https://github.com/justinvyu/oil-spill

Technologies Used

Tensorflow, NumPy, Matplotlib

Abstract

Oceanic oil spill pollution poses a serious threat to marine ecosystems. Undetected spills from accidents or operational discharges from ships can harm marine life residing on the sea surface or on shore. Previous studies try to automatically detect spills using remote sensing imagery from synthetic aperture radars. However, the accuracy of the traditional algorithms is limited by the presence of look-alike biogenic films that have overlapping physical features with true oil spills. Difficulties remain in identifying useful features and their combinations to distinguish between the two categories. Here, we proposed a methodology based on a genetic algorithm to address this challenge. This procedure finds an optimal or near-optimal solution within a given search space by mimicking the natural processes of competition, reproduction, mutation etc. Our procedure also addresses the premature convergence problem commonly found in genetic algorithms. We tested the procedure on simulated datasets using published statistics, and our results show an average accuracy of 88.2% for oil spills, representing a statistically significant improvement over the literature (~82%). The optimized classification also reduces the time spent on look-alikes, allowing for a faster response to minimize environmental damage.

Figures

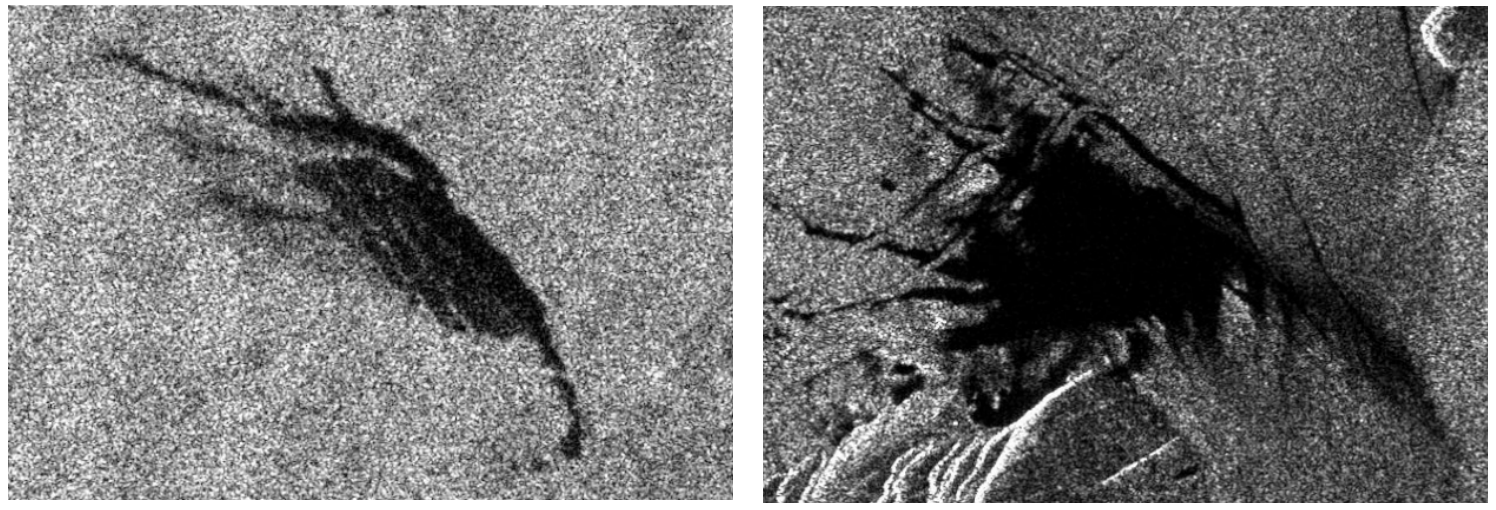
Oil Spill (left) vs. Lookalike Ocean Film (right)

It's hard for the human eye to distinguish oil spills and lookalikes films in the water from satellite radar imagery. Ideally, an autonomous system would be able to accurately flag oil spills and send coastal cleanup crews.

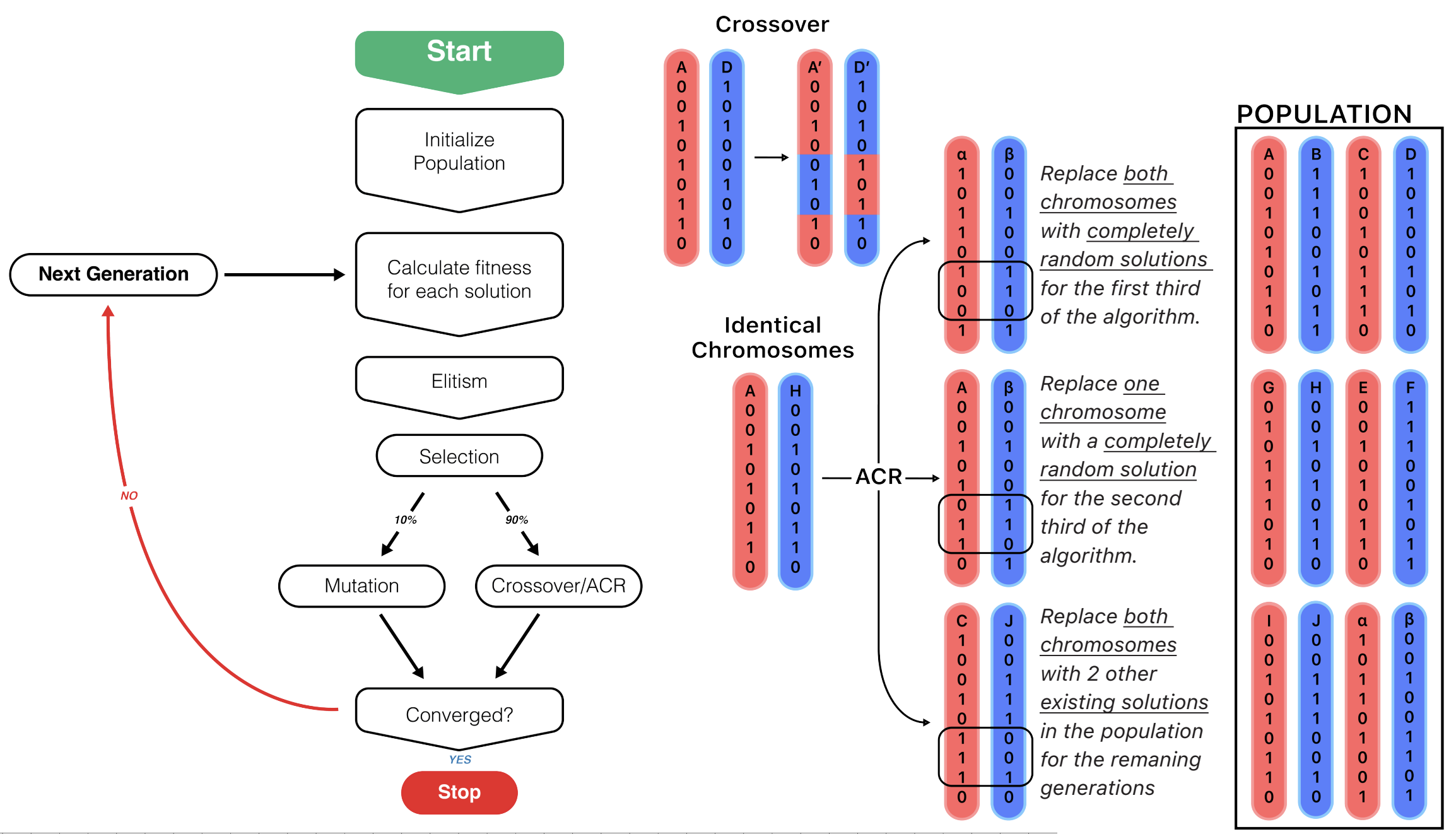
Genetic Algorithm Diagram

Algorithm composes of four main steps:

1. Elitism (the best "genes" of each generation is passed on)
2. Selection (remaining gene pool competes to survive)
3. Mutation (random chance)
4. Crossover (current generation "reproduces" to create a generation with mixed genes)

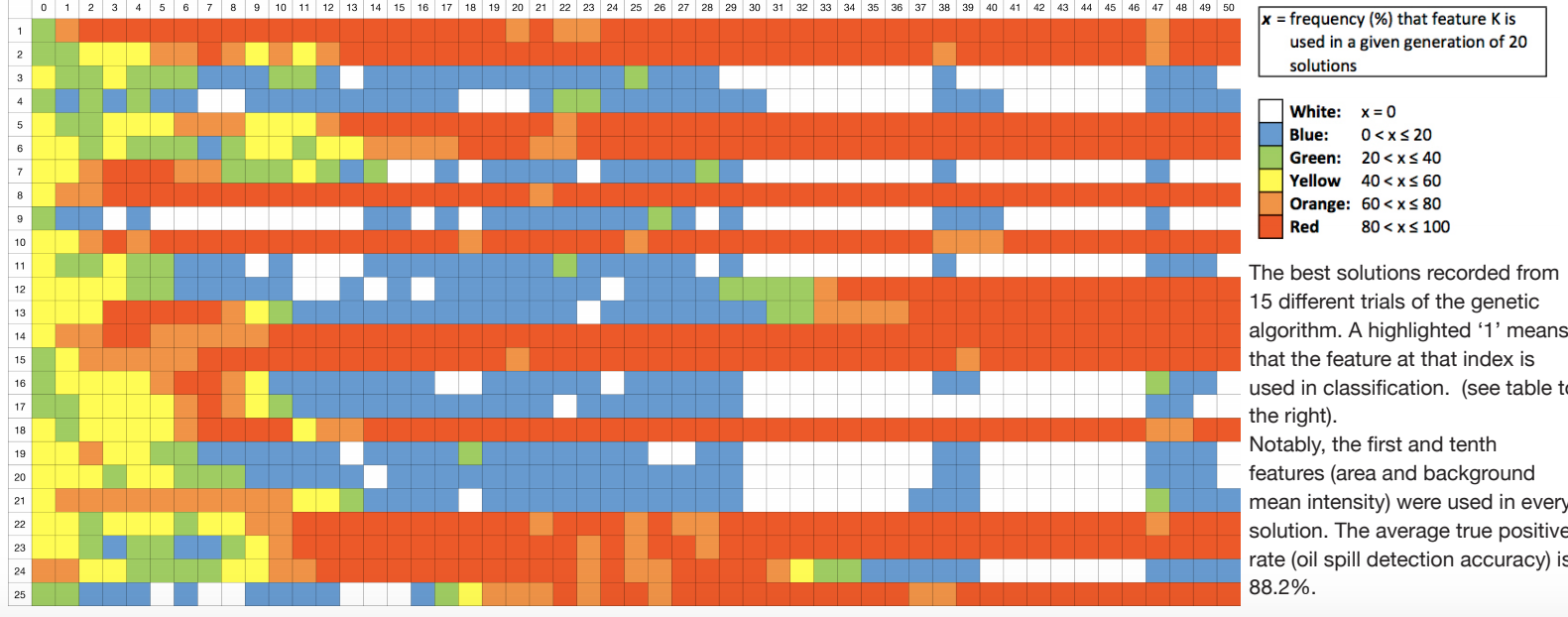
Emergence of optimal features

The evolution of feature usage over the course of a single run (50 generations) of the genetic algorithm. For every feature K, the frequency that it is used is calculated by taking the number of appearances in the population divided by the population size, and the corresponding cell is colored according to the legend on the right.

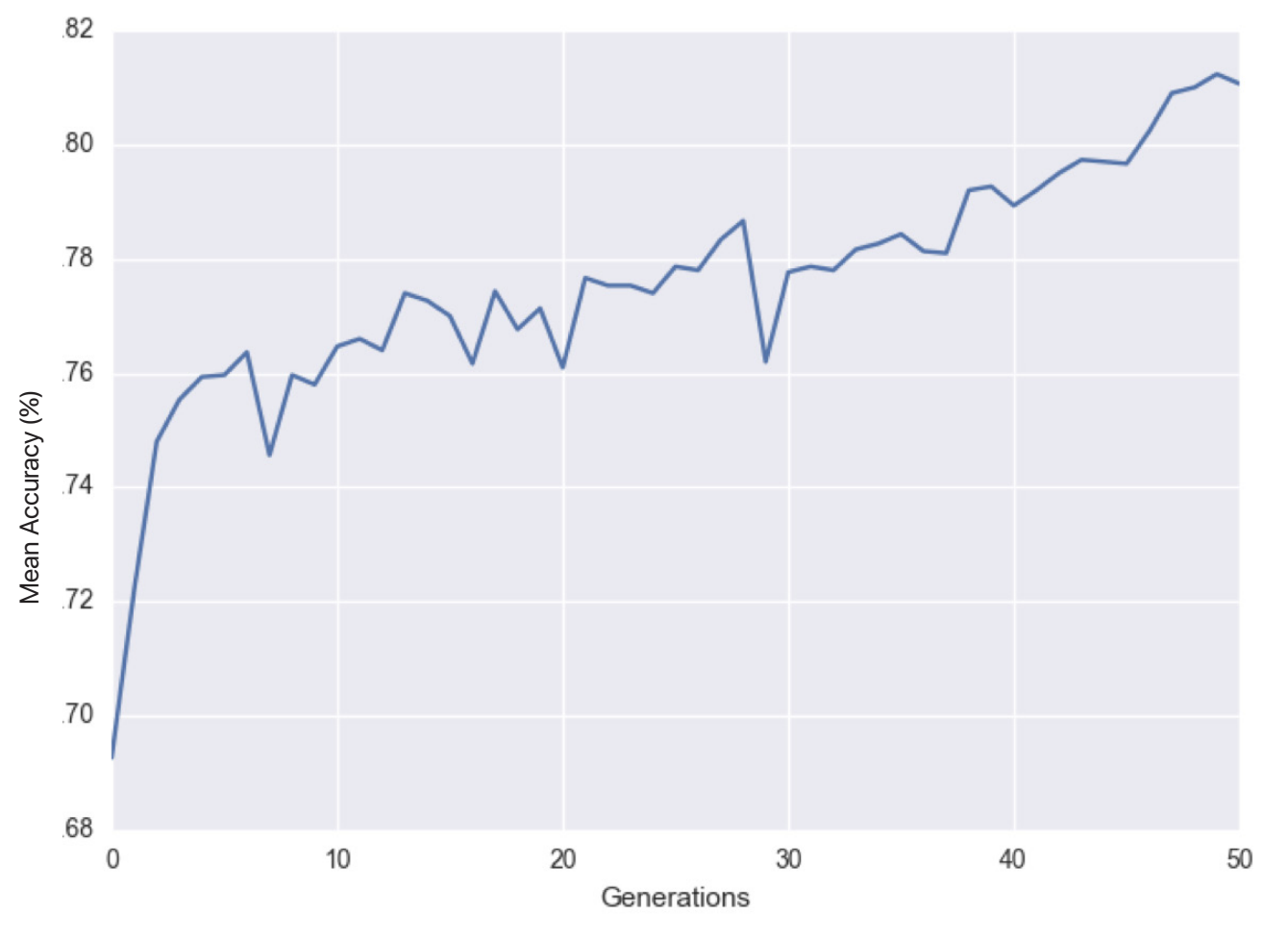
Learning curve over 50 generations

The mean classification accuracy of the population of solutions throughout the course of one trial (50 generations): ranges from around 69% to 81% in overall accuracy for an improvement of 12% accuracy from the original population.

Method

My paper introduced a method called Adaptive Chromosome Replacement, which is a form of an exploration bonus for a genetic algorithm. It accomplishes this by randomly injecting noise into generations, when the overall population and gene pool have become too stagnant.

def cross(self, generation, male, female) :
    locuses = random.sample(range(0, male.length() - 1), 2)
    locus_left = min(locuses)
    locus_right = max(locuses)

    child_1 = deepcopy(male)
    child_2 = deepcopy(female)

    # Adaptive Chromosome Replacement (ACR)
    if child_1.fitness == child_2.fitness:
        if generation < int(self.NUMBER_OF_GENS / 3):
            child_1 = Chromosome(Trainer.n_features)
            child_2 = Chromosome(Trainer.n_features)
        elif generation < int(2 * self.NUMBER_OF_GENS / 3):
            child_2 = Chromosome(Trainer.n_features)
        else:
            child_2 = self.random_chromosome()

    child_1.replace_range(female, locus_left, locus_right)
    child_2.replace_range(male, locus_left, locus_right)

    return [child_1, child_2]